Hardware-Friendly Implementation of the Correlated
Pink Noise Generator
Background
The stochastic pink noise generator algorithm as described on the
newpink.htm page generates a pink process
that can take on any value in a continuous range. Many physical
processes have a similar property. But it is not a property necessary
for "pinkness." As mentioned there briefly, Andreas
Robinson observed that the choice of a 2-valued distribution
for each generator results in an algorithm in which most of the
arithmetic operations disappear. If all you really care about is
generating the right kind of power spectrum, and you don't care about
the choppy distribution of signal levels, this might be just what you are
looking for.
Software Implementation
The idea is clearest in a software-oriented implementation that
you might consider if you are going to drive a digital-to-analog
converter device directly from a parallel digital port. Andreas refers
back to the original algorithm using a uniform distribution:
So, if you constrict ur2 to be either 0 or 1 (i.e binary),
all sorts of interesting things happen.
First, the speed of an LFSR white random number generator [increases],
since ur2 = rand requires a single random bit, rather than the 15
bits that are typical.
Second, you can see that you do not really need the multiplication
anymore. The C code would look like this:
contrib[stage] = ur2 ? pA[stage] : 0;
(Actually it is
contrib[stage] = ur2 ? pA[stage] : -pA[stage];
but it makes little practical difference.)
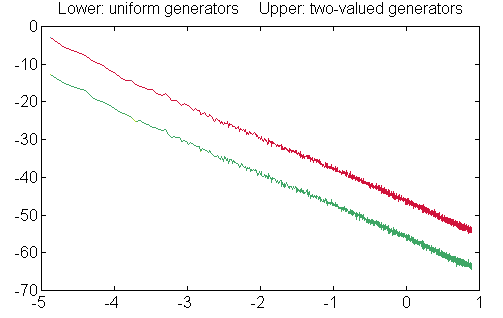
If there is any doubt that this scheme works, the following plot
compares the output results from using uniformly-distributed and two-
valued randomized generator stages. Both the response level on the vertical
axis and the frequency on the horizontal axis are logarithmic. You can
see that the only significant difference in the spectrum is a constant
gain factor.
For hardware-oriented applications, using 0 or
+pA[stage] for the output levels as he suggests offers some
minor practical advantages. An output range from 0x0000 to
0xFFFF rather than 0x8000 to 0x7FFF needs a little less tweaking to
drive D-to-A converters directly. You won't care about the output bias
if you capacitively couple the final output signal — not a bad
idea anyway.
In addition to this simplification in the updating logic, the
arithmetic to sum the contribution of the generator stages can be
avoided as well.
As a consequence genout = sum(contrib) will only return
one of 2^5 = 32 possible sums, so why not put them in a table?
The output data table can be built by hand and placed into static
storage without much difficulty, but Andreas provides the following
algorithm in C for offline analysis to generate the data. This is only
done once to initialize the data arrays.
void Setup()
{
const double pA[] = { 3.80240, 2.96940, 2.59700, 3.08700, 3.40060 };
double pASum = 15.8564;
int i;
// Build lookup-table
for (i = 0; i < 32; i++)
{
gensum[i] =
((((i & 1) != 0) ? pA[0] : 0) +
(((i & 2) != 0) ? pA[1] : 0) +
(((i & 4) != 0) ? pA[2] : 0) +
(((i & 8) != 0) ? pA[3] : 0) +
(((i & 16) != 0) ? pA[4] : 0));
gensum[i] = (gensum[i] / pASum) - 0.5;
}
}
As a practical matter, the final generator outputs are going to be
used as fixed point values anyway, driving a digital port, so you
might as well scale the result for the output range you want in fixed
point. Observing, as Andreas did previously, that you probably don't care
about DC offsets, you can scale to the maximum 16-bit output range
[0,65535u] for a 16-bit output converter as follows.
gensum_fixed[i] = (unsigned int)(gensum[i]*65536.0/pASum);
The Runtime Code
Andreas suggested the following code, implementing the 2-valued generator
approach in double precision like the original algorithm description.
double GetPinkValue()
{
const double pSum[] = { 0.00198, 0.01478, 0.06378, 0.23378, 0.91578 };
extern int gsidx;
extern double gensum[];
int i;
double ur1 = Rand(); // Returns random 0.0 to 1.0
int ur2 = Rand1(); // Returns random single bit
for (i = 0; i < 5; i++)
{
// Find the bit to be updated
if (ur1 < pSum[i])
{
// Clear selected bit in the global index variable
gsidx &= ~(1 << i);
// Replace it with a new randomized bit value
gsidx |= ur2 << i;
// Exit loop, do not update any other bits!
break;
}
}
return gensum[gsidx];
}
Variable gsidx preserves the states of the generators
from one pass to the next. During the course of the algorithm, the bits in gsidx
are adjusted to select the appropriate entry of the table previously
computed. The final line extracts the tabulated value.
If you are implementing this with a fixed-point processor, there are
a few more variations you can try.
After Andreas's implementation eliminates almost all of the
arithmetic, the double precision no longer buys much. You could
operate in fixed point directly. Compiler-supported 16-bit
arithmetic remains necessary for testing the cumulative probability
levels.
Andreas trusts his compiler to optimize loops well. If it does
that, the loop disappears! A really smart compiler
will be able to unroll the loop. In the logic sequence that remains,
at most one update is applied per call. For the truly paranoid who
don't trust compilers and never will, you can unroll the loop
manually.
If you use a bitwise randomizer for pseudo-random number
generation (Andreas uses a Linear Finite Shift Register), you can
use the first 15 bits for the selection of the generator stage for
updating, and the last bit for determining whether the selected
generator stage toggles or not. For this special case (and we do have to be
careful) one of the random generator calls can be avoided.
The evaluation order of the tests can be reversed, as suggested
in the algorithm description page, to test
generators in the order from most likely to update to the least likely.
There is a marginal speed improvement that results from avoiding some
testing arithmetic.
When updating uniformly distributed generators, the probability
of repeating the same value twice is vanishingly small. But this changes
completely with the two-valued generators — the probability that
a generator keeps the same output value is 50%! Taking advantage of
this detail, we can check for the case that nothing changes first, and
avoid about half of the logic computations.
With these variations, things occur in a different order so the
code looks different, but the effect is the same.
// Determine the current pink signal output value
unsigned int GetPinkValue()
{
const unsigned pSum[] = { 130u, 1098u, 4180u, 15320u, 60016u };
unsigned ur = Rand(); // Returns uniform random 0 to 65535u
unsigned mask = 0x10; // Start processing from last generator
extern unsigned gsidx;
extern unsigned gensum_fixed[];
do {
// There is a 50-50 chance that updating a 2-valued stage won't
// change anything. Take advantage of this special case first!
if ( ur & 1 ) break;
// There is a small probability that no generators change anyway.
if ( ur > pSum[4] ) break;
// If that didn't happen, find the right generator and toggle it.
ur > pSum[3] ? gsidx ^= mask, break : mask >>= 1;
ur > pSum[2] ? gsidx ^= mask, break : mask >>= 1;
ur > pSum[1] ? gsidx ^= mask, break : mask >>= 1;
ur > pSum[0] ? gsidx ^= mask, break : mask >>= 1;
gsidx ^= mask;
} while (0); // Never loops back!
return gensum_fixed[gsidx];
}
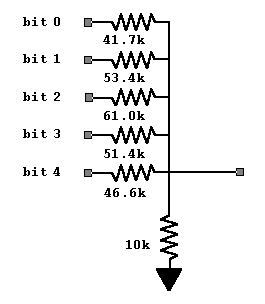
A Hardware Implementation
In Andreas's first implementation, the output lookup table
converts the patterns of 5 on/off bits into longer patterns of on-off
bits suitable for a digital data file or for driving a converter
hardware port. Digital to analog conversions are typically done using
resistors with value 1R, 2R, 4R, etc. — the lower the
resistance, the more current that flows when the corresponding bit
becomes active high. The sum of the currents is then converted to a
voltage.
But Andreas observed that this kind of geometric progression is
not necessary. You can eliminate the D-to-A device and apply appropriate
non-binary weights for the five on-off generator bits directly.
The scaling values from the general algorithm description are:
pA = [ 3.8024 2.9694 2.5970 3.0870 3.4006 ]
|
You can apply these scaling values by picking special
resistance values in a resistor network. To keep the current paths
for each bit independent, usually an operational amplifier is used.
However, Andreas has done an analysis to account for the interactions
among the signal lines in the resistor network, thus avoiding the
operational amplifier. I have verified his design, but if you want to
verify it for yourself, you can find the full details with exact
design values in his pinkgen.c code. If you
would like, you can compare to his hand-optimized 8-bit AVR
microcontroller implementation
avr-pinkgen.asm in assembler, which also
addresses timing considerations.
|
Once you have this circuit built, all you have to do is connect it
directly to the bits on a parallel digital output port. The output table
used to drive an ordinary digital-to-analog converter is no longer
necessary. Just send the computed "index" variable straight to the port.
// return gensum[gsidx]; No longer needed!
parallel_write(port, gsidx);
Back to the general algorithm description
Back to the technology index
Site: RidgeRat's Barely Operating Site http://home.earthlink.net/~ltrammell
Author: Larry Trammell Created: Jan 19, 2006 Revised: Jan 07, 2007 Status: Experimental
Contact: NOSPAM ltramme1476 AT earthlink DOT net NOSPAM
Related: See the 'definitive pink noise site' at http://www.firstpr.com.au/dsp/pink-noise/
Restrictions: This information is public domain.
Thanks to Andreas Robinson for contributing his ideas and code.

